20 Semi-Parametric Regression with splines
20.0.1 Basis functions
The quadtratic model: \[y_{i} = \beta_{0} +\beta_{1}x_{i} + \beta_{2}x_{i}^2 + \epsilon_i \]
- The basis for this model are the functions 1, x, and \(x^2\) \[ X = \begin{bmatrix} 1 & x_{1} &x_{1}^2 \\ \vdots & \vdots & \vdots \\ 1 & x_{n} & x_{n}^2 \end{bmatrix} \]
20.0.2 Example
n=30; x=sort(runif(n,0,2)); b0=1; b1=2; b2=4; b3=-1
y=c(b0+b1*x[x<=1],b2+b3*x[x>1])+rnorm(n,0,0.1)
plot(x,y,xlim=c(0,2),ylim=c(0,3.2),las=1); library(KernSmooth)## KernSmooth 2.23 loaded
## Copyright M. P. Wand 1997-2009plot(x,y,xlim=c(0,2),ylim=c(0,3.2),las=1); abline(v=1,lty=3)
abline(lm(y~x),col=2);preg=lm(y~x+I(x^2)); lines(x,preg$fit,col=4);
lfit=locpoly(x, y, degree=2,band= 0.25); lines(lfit,col=3)
20.0.3 Broken Stick Model
\(y_i = \beta_0 + \beta_1x_i + \epsilon_i \text{ if } x_{i} \le 1\) \(y_i = \beta_2 + \beta_3x_i + \epsilon_i \text{ if } x_{i} > 1\)
For any real number u, the positive part is a truncated line
v=seq(0,2,length=100); plot(v,pmax(v-1,0),type="l",ylab="")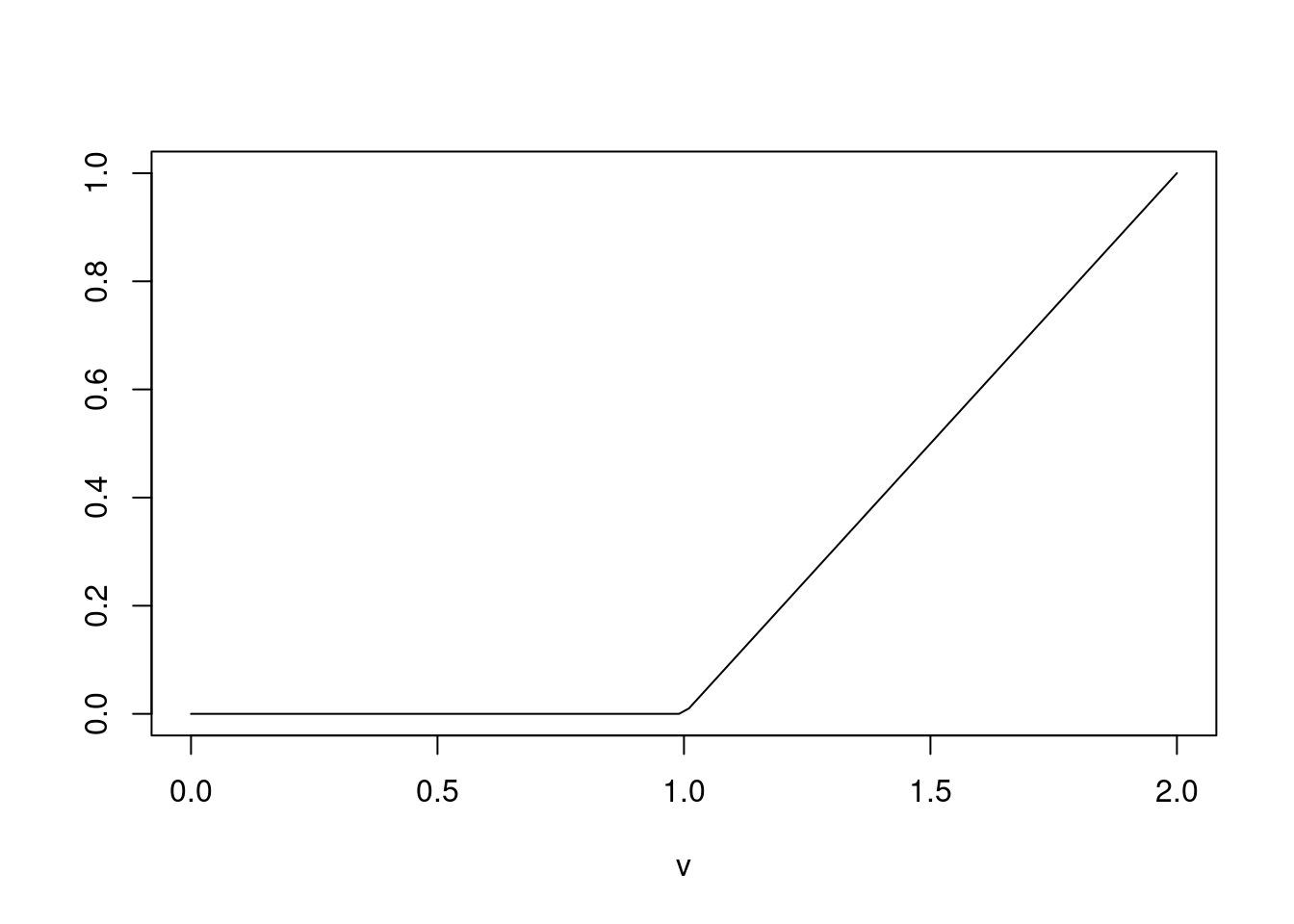
We add a basis function:
- 0 to the left of 1;
- a positively sloped function from 1 onward
Model: \(y_i = \beta_0 + \beta_1{x_{i}} + \beta_{11}(x_{i} - 1) + \epsilon_i\)
- If \(4 x_{i} \le 1, y_i = \beta_0 +\beta_1{x_{i}} + \epsilon_i\)
- If \(x_i > 1\),
\(y_i = \beta_0 + \beta_i{x_i} + \beta_{11}(x_{i} -1) + \epsilon_i \\ (\beta_0 - \beta_{11}) + (\beta_1 + \beta_{11})x_{i} + \epsilon_i\)
\[ X = \begin{bmatrix} 1 & x_{1} &(x_{1}-1) + \\ \vdots & \vdots & \vdots \\ 1 & x_{n} & (x_{n} -1) + \end{bmatrix} \]
plot(x,y,xlim=c(0,2),ylim=c(0,3.2),las=1); abline(v=1,lty=3)
lines(lfit,col=3); pmx1=pmax(x-1,0)
breg1=lm(y~x+pmx1); lines(x,breg1$fit,col=2)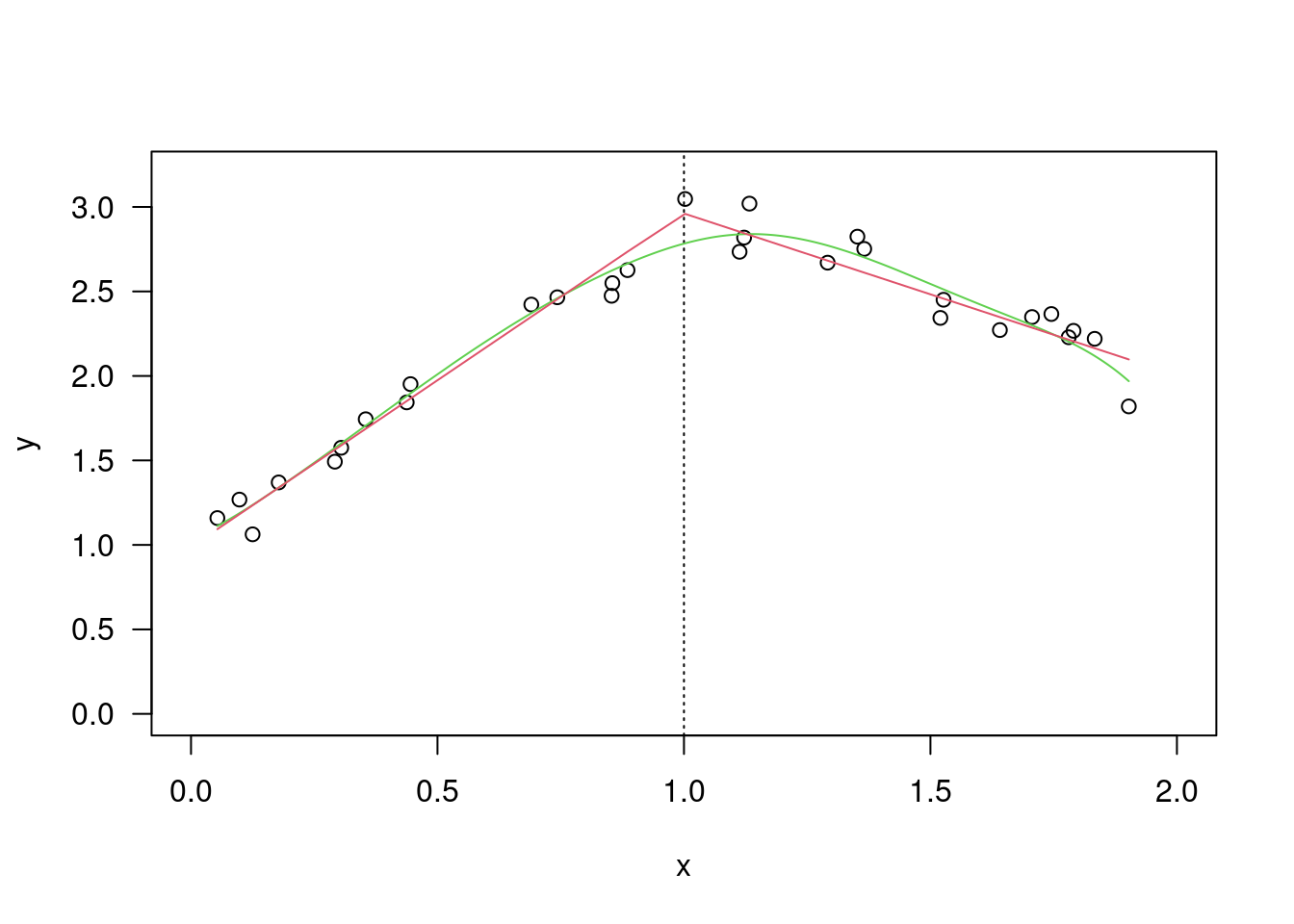
n=30; x=sort(runif(n,0,3));
yf=function(x){
b0=1; b1=2; b2=4; b3=-1; b4=0; b5=1;
c(b0+b1*x[x<=1],b2+b3*x[(x>1)&(x<=2)],b4+b5*x[x>2])
}
y=yf(x)+rnorm(n,0,0.1);
xs=seq(0,3,length=100);
ys=yf(xs)
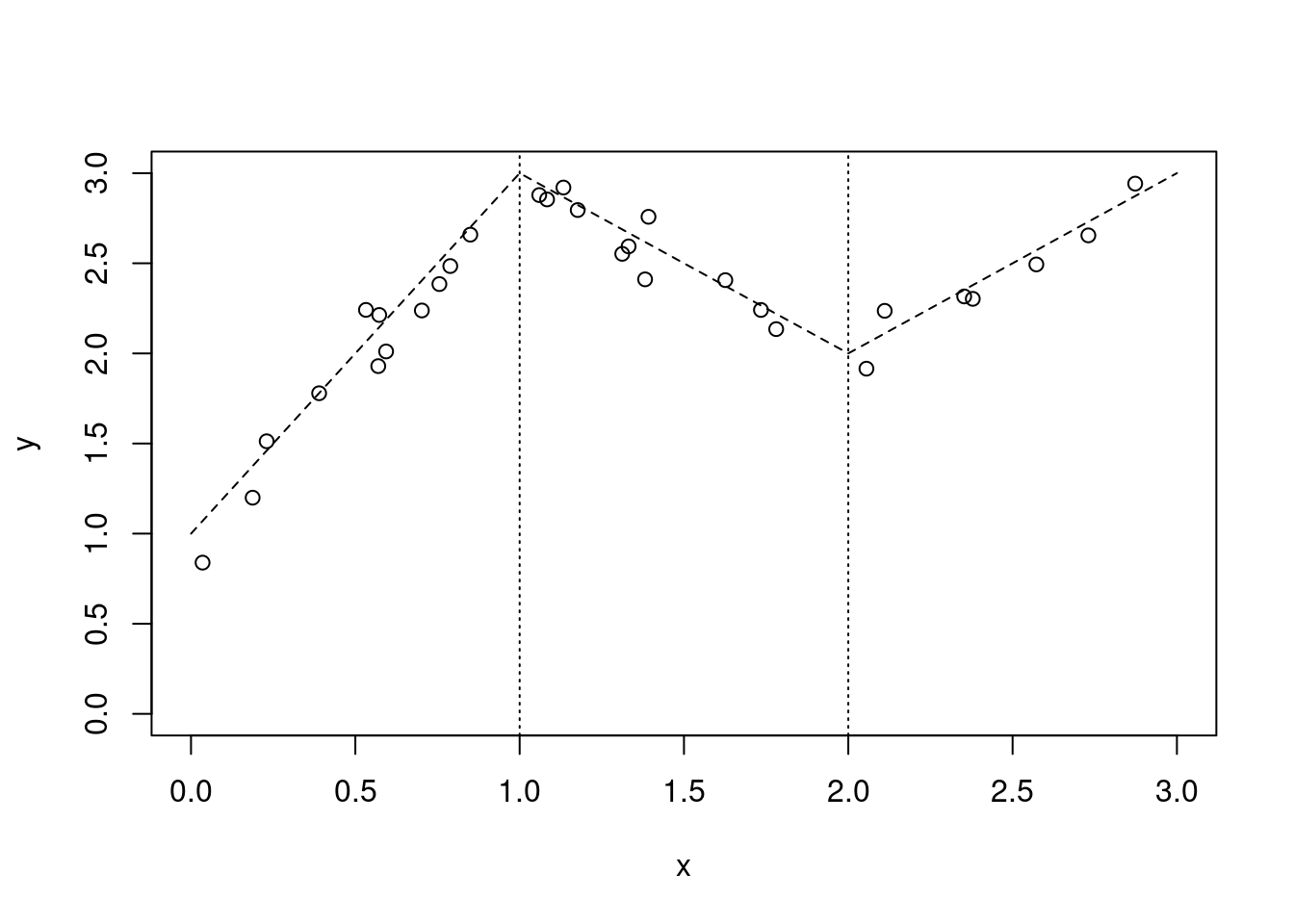
plot(x,y,xlim=c(0,3),ylim=c(0,3)); abline(v=c(1,2),lty=3);
lines(xs,ys,lty=2);